昨天有介紹PCA的降維和分群應用,那這邊再提一下PCA和分群方法有什麼不同。
首先, PCA 和各種「分群」都是屬於非監督是學習的機器學習方法,但是:
PCA looks to find a low-dimensional representation of the observations that explain a good fraction of the variance.
Clustering looks to find homogeneous subgroups among the observations
今天主要想介紹的是「分群 Clustering」的機器學習方法,K-means。
K-means 是一種分群的方法,假設今天我們不知道這筆資料集內各資料分別是什麼類別,我們想將整個資料大致分成 K 類/群 時,可以使用 K-means 分群方法。
K-means 分群的計算想法是希望「群內的變異」要盡可能的小。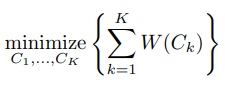
想計算變異量時,常常會透過計算squared Euclidean distance進行數值量化。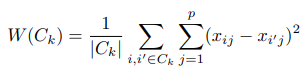
演算法流程:
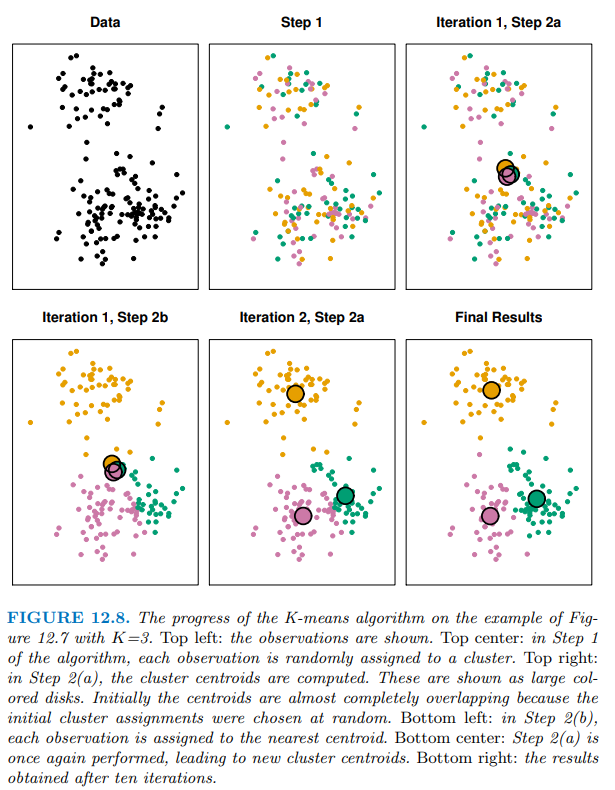
K 值的選擇
[R code]
使用的 kmeans( data, k, nstart )函式進行 K-means 分群。
nstart 指的是嘗試 n 種隨機配置生成的初始中心,提供最佳初始中心。
建議設置 20 或 50 ,至少有一定的大小,不要設 1 。
由於二維資料比較容易以圖形展現結果,這邊示範將隨機生成的二維資料(X) 分群。
## 隨機生成 50 筆二維資料(X)
set.seed (2)
x <- matrix ( rnorm (50 * 2), ncol = 2)
x[1:25, 1] <- x[1:25, 1] + 3
x[1:25, 2] <- x[1:25, 2] - 4
[,1] [,2]
[1,] 2.103085 -4.838287
[2,] 3.184849 -1.933699
[3,] 4.587845 -4.562247
[4,] 1.869624 -2.724284
[5,] 2.919748 -5.047573
[6,] 3.132420 -5.965878
...
分成兩群(k=2):
km.out <- kmeans (x, 2, nstart = 20)
km.out$cluster # 分群結果,分成哪群
plot (x, col = (km.out$cluster + 1),
main = "K- Means Clustering Results with K = 2",
xlab = "", ylab = "", pch = 20, cex = 2)
> km.out
K-means clustering with 2 clusters of sizes 25, 25
Cluster means:
[,1] [,2]
1 3.3339737 -4.0761910
2 -0.1956978 -0.1848774
Clustering vector:
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2
[27] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
Within cluster sum of squares by cluster:
[1] 63.20595 65.40068
(between_SS / total_SS = 72.8 %)
Available components:
[1] "cluster" "centers" "totss"
[4] "withinss" "tot.withinss" "betweenss"
[7] "size" "iter" "ifault"
km.out$tot.withinss: Total within-cluster sum of squares.(整體資料的 sum of squares)km.out$withinss : The individual within-cluster sum-of-squares.(各群內分別的 sum of squares)
> km.out$tot.withinss
[1] 128.6066
> km.out$withinss
[1] 63.20595 65.40068
分群結果: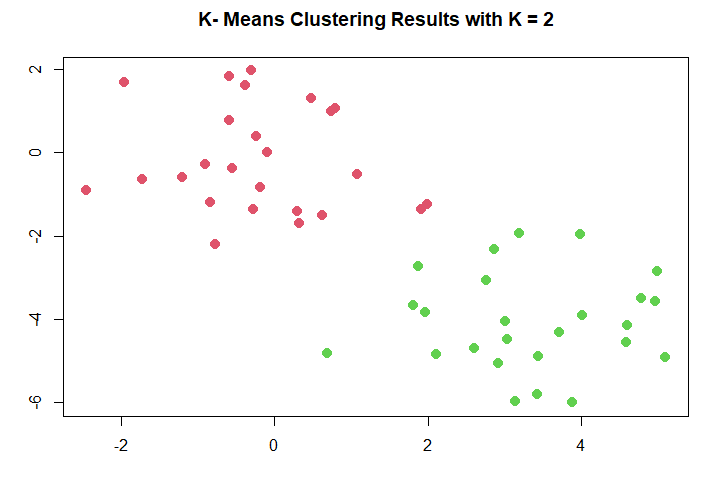
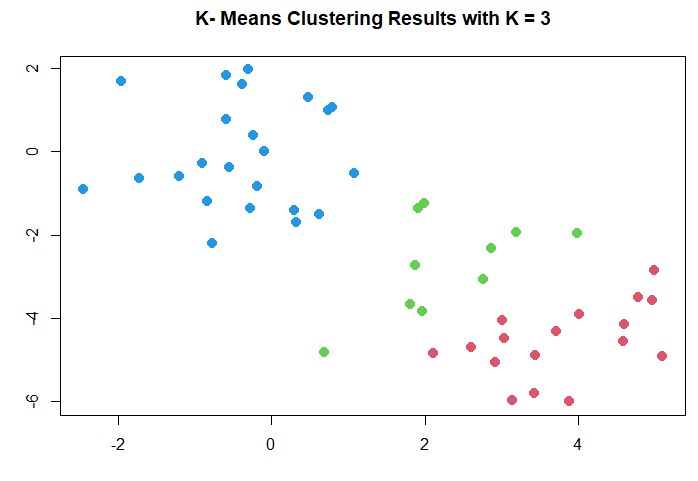
分成三群(k=3):
km.out <- kmeans (x, 3, nstart = 20)
km.out
plot (x, col = (km.out$cluster + 1),
main = "K- Means Clustering Results with K = 3",
xlab = "", ylab = "", pch = 20, cex = 2)
# NCI60 data
library (ISLR2)
nci.labs <- NCI60$labs
nci.data <- NCI60$data
dim(NCI60$data)
table(nci.labs )
dim(iris)
# 標準化資料scale the data
sd.data <- scale(nci.data)
## k-means 分群(clustering)
set.seed (2)
km.out <- kmeans (sd.data, 4, nstart = 20) # 4 cluster
km.clusters <- km.out$cluster # 得到分群結果
## PCA
pr.out <- prcomp (nci.data , scale = TRUE)
# 在 pc1, pc2 axis上呈現k-means分群結果 (對照真實cancer types)
par (mfrow = c(1, 2))
Cols <- function (vec) {
cols <- rainbow ( length ( unique (vec)))
return (cols[as.numeric (as.factor (vec))])
}
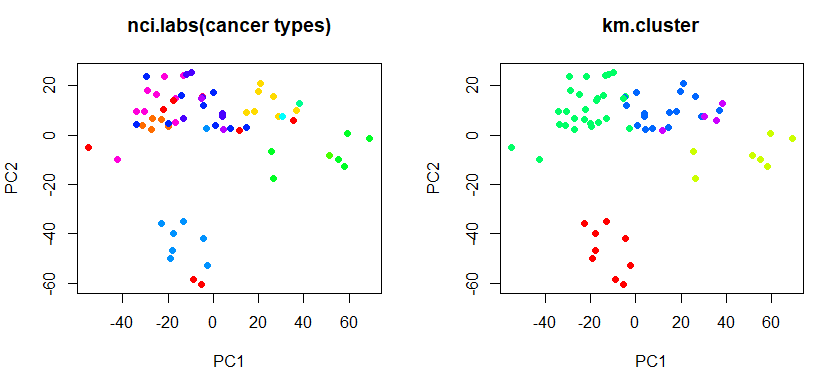
# show cluster on pc1, pc2 axis
plot (pr.out$x[, c(1, 2)], col = Cols (nci.labs), pch = 19,
main = "nci.labs(cancer types)")
plot (pr.out$x[, c(1, 2)], col = Cols(km.clusters), pch = 19,
main = "km.cluster")
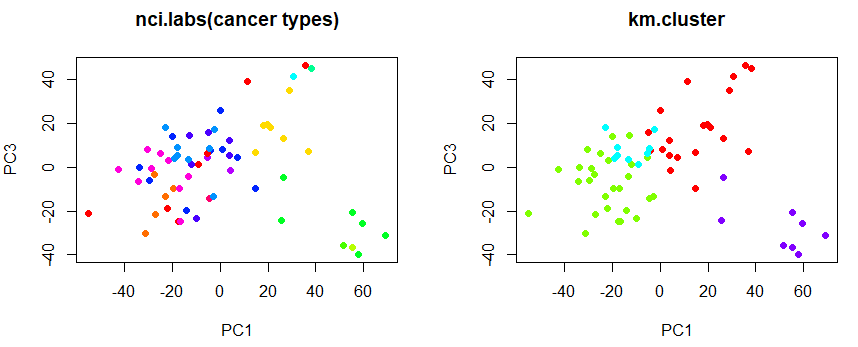
# show cluster on pc1, pc3 axis
plot (pr.out$x[, c(1, 3)], col = Cols(nci.labs), pch = 19,
main = "nci.labs(cancer types)")
plot (pr.out$x[, c(1, 3)], col = Cols (km.clusters), pch = 19,
main = "km.cluster")
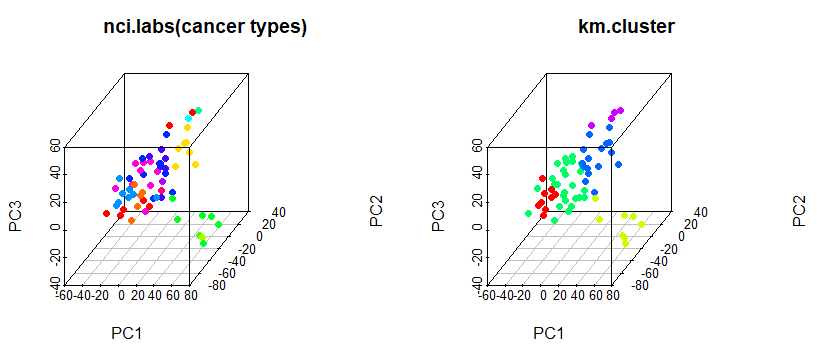
# 3d plot
# install.packages("scatterplot3d")
library(scatterplot3d)
scatterplot3d(pr.out$x[, c(1,2,3)], pch = 16, color = Cols(nci.labs), main = "nci.labs(cancer types)")
scatterplot3d(pr.out$x[, c(1,2,3)], pch = 16, color = Cols(km.clusters), main = "km.cluster")
K-medoids 也是一種分群的非監督是機器學習方法,和 K-means 不同, 分群計算迭代時不是計算平均值,而是計算群中的 medoid,計算距離並非用 Euclidean distance,而是去計算兩兩(樣本、中心)之間的距離和。
K-medoids 演算法:
| 比較 | K-means | K-medoids |
|---|---|---|
| 中心點 centroid | 虛擬點(平均) | 實際樣本點(中位數概念) |
| 迭代重新找中心點的方式 | 群內樣本平均值 | 中心點和群內樣本之間的距離和最小 |
| 優缺點 | 只能處理連續數值資料 | 可以同時處理連續和類別型資料 |
| 計算速度快(適用於較大的資料量) | 比較穩健(Robust)不怕離群值、計算量龐大(適用於較小的資料量) |
An Introduction to Statistical Learning with Applications in R. 2nd edition. Springer. James, G., Witten, D., Hastie, T., and Tibshirani, R. (2021).
The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd edition. Springer. Hastie, T., Tibshirani, R. and Friedman, J. (2016).
[機器學習首部曲] 聚類分析 K-Means / K-Medoids (@PyInvest)
https://pyecontech.com/2020/05/19/k-means_k-medoids/
E.M. Mirkes, K-means and K-medoids applet. University of Leicester, 2011.
http://www.math.le.ac.uk/people/ag153/homepage/KmeansKmedoids/Kmeans_Kmedoids.html
